点击蓝字 关注我们

在这次创新更新专栏里,我将介绍一种方法,即借助人工智能和自动化手段,把本福德定律的应用推进到更高的层次,从而让反舞弊调查人员可以运用本福德子集差异分析(BSDA)。这种方法可以帮助我们找出那些在本福德定律下表现得最不符合预期的子集,比如不同的业务部门、开支类型、供应商分类等,而不必逐个使用费时的筛选条件来审查整个数据集。我有幸与Nigrini合作,深入探讨了这一理念,并在他指导下对几个场景进行了测试。
简要介绍一些理论背景
根据去年《科学美国人》的一篇文章,本福德定律最早是在1881年由天文学家Simon Newcomb发现的。物理学家Frank Benford在1938年再次观察到了这一现象,并使这一定律广为人知,同时将其命名为本福德定律。有些文献中提到该定律时会同时使用两个名字,称为“Newcomb-Benford定律”。它也被称为“异常数定律”。在很多实际生活中的自然数集合里,首位数字往往是较小的数字,比如1、2或3等。在符合该定律的数据集中,数字1作为首位数字出现的频率大约是30%,而9作为首位数字出现的频率则低于5%。以下是1至9作为首位数字的概率(尽管在某些情况下我们确实需要零,比如0.07,但零不能作为首位数字)。
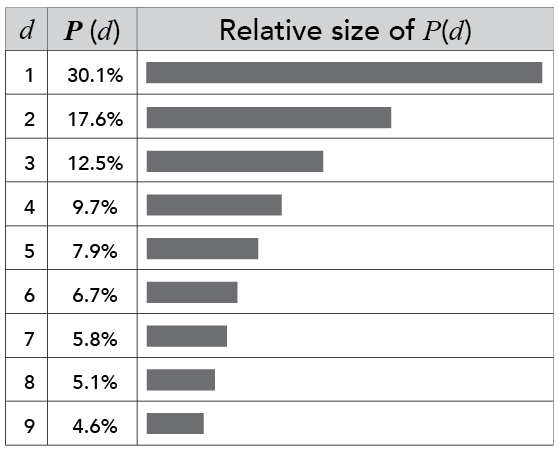
图1:本福德的第一位数概率
针对财务数据,与本福德定律相关的最有效测试方法是前两位数字测试,这种方法可以减少突出项目的样本量。此测试尤其适用于发现大量接近但略低于内部控制系统设定或被认为的阈值的交易,比如公司规定超过5,000美元的发票需要第二个人批准或提供额外文件才能付款。这促使了舞弊者将发票金额控制在这个数额之下,比如4,900美元甚至4,999美元,以避开阈值限制。在图2中,你可以观察到以“49”和“48”开头的发票数量出现了异常增长。理论上,这类数字组合应该只占总数的大约0.89%,但实际数据显示它们约占1.1%,形成了明显的峰值。这表明可能存在人为因素将发票金额刻意保持在5,000美元的阈值之下。
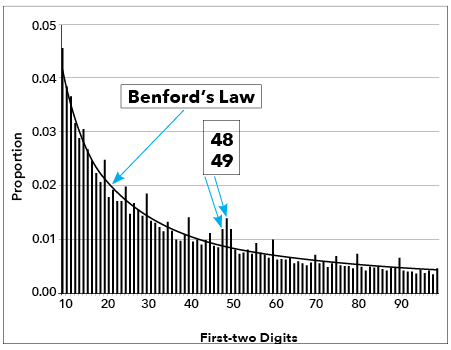
图2:两位数示例
在与Nigrini的访谈中,他提到本福德定律能够帮助舞弊检查员或审计师识别以下几种情形:
识别大量的虚构日记账项,它们的金额通常低于审计测试的阈值或公司的规定限制。
发现数据中的“峰谷现象”——即在图表中,如果数据点集中在本福德定律预期线的上方或下方,则可能是人为制造了大量数据或虚构条目的信号。
检测总账中的异常情况,比如同一金额的交易出现异常高的重复次数。这些异常虽然不一定意味着舞弊,但可能是由于错误造成的。
现有方法存在的难题
尽管本福德定律在分析数据集时既简单又有效,但它确实有一个局限:即它以一种聚合和线性的方式处理大规模数据集。Nigrini建议,使用前两位数字测试时,舞弊审查人员应该分析至少包含2,500笔交易,最好是超过5,000笔交易的数据集。对于大型全球企业来说,获取5,000笔交易的数据非常容易,因为它们的日记账条目可以覆盖成千上万,甚至是数百万笔交易。然而,真正的挑战在于如何在小规模业务单元中,或者在特定地理区域内的一群人中,从大量交易中识别出异常行为。由于当前交易量巨大,那些不符合本福德定律的风险交易很容易被“淹没”。

数据可视化工具如Tableau或PowerBI能帮助我们根据具体案例,通过地理区域、费用类型或其他标准来筛选大规模的数据集。目的是精确地识别出汇总数据中的某个子集中可能出现的异常行为,从而在不同阈值下发现异常情况。不过,鉴于地理区域、业务部门、费用类型、支付方式及其他因素之间的过滤组合可能达到数百甚至数千种,这种方法仍然非常耗时。
但如果可以让机器自动执行所有这些筛选场景,而不是逐一人工进行过滤呢?
人工智能增强手段
与Nigrini讨论时,针对手动运行多组过滤条件来发现异常所面临的挑战,我们提出了自动化这一流程的想法,旨在专门识别那些造成最大本福德定律偏离的特定子集。为此,我和Kona AI的数据科学主管Roopak K. Prajapat一起工作,分析了一个涉及数十万张发票支付、总金额超过30亿美元的大规模数据集。总体来看,这些汇总数据基本符合本福德定律,但其中也存在一些显而易见的例外情况,比如以“20”和“21”开头的支付数据显得特别突出。
接下来,我们采用了本福德子集差异分析(BSDA)以及包含机器人流程自动化(RPA)元素的自动化技术,针对五个特定分类运行数据,以识别出在满足至少5,000个最小样本量要求的情况下,偏离本福德定律最显著的子集。我们在测试过程中考虑的变量包括:
供应商分类。
支付方式。
国家地区。
总账科目。
文件类型。
该模型在普通的硬件设备上,仅用了约21分钟就处理了超过17,808种不同的组合,从而找出了偏差最大的子集。(与手动处理所需的时间相比,这大大缩短了分析周期。)
最显著的异常子集是某个特定供应商——为了保密,这里不具体提及——其特征如下表所列。

随后,我们将这些交易数据输入到一个预测性机器学习模型中,目的是找出统计上与之类似的“更多类似于此”的交易,以进一步优化分析结果。经过改进的本福德分析在这个特定子集中发现了大量不同类型的异常现象。
重要观察
异常情况:图表中显著的红色峰值,特别是在像11、14、29、43、58、72、87这样的数字周围,显示某些交易出现的频率远超本福德定律的预期。这些峰值是潜在异常或不规范行为的警示信号。
潜在风险:与预期分布的偏差可能暗示了数据篡改、舞弊行为或某些需要进一步调查的具体交易模式。这些显著的峰值可能表明,在此总账科目下记录的交易中存在人为调整或系统性的偏见。
合规关注:由于本福德定律常被用于舞弊检测,此次分析中显著的偏差提示我们,“N-US SUB USD NETTING”总账科目下的交易可能需要更加严密的审查。这可能包括调查为什么某些交易或类别相比其他交易显得异常频繁。
等距异常:显著的视觉模式显示,这些异常情况彼此之间的间隔大致相同。深入探究这些现象背后的成因,有助于发现更多有价值的信息。
我们已经将这些交易数据提交给客户进行调查,客户认为这些交易异常到足以启动正式调查,目前调查仍在进行中。负责此案的调查人员不仅要审查供应商CCUS10,还应该扩展到相关的子集,比如2023年和2022年的交易记录,以及记入相同费用或资产账户的开支情况。

未来的本福德定律
本福德定律一直是一个有用的舞弊检测工具,并将继续保持其重要性。随着更好的技术和自动化方法的应用,如本福德子集差异分析(BSDA)等技术使得调查人员能够迅速而高效地识别出最异常的数据子集。这将原本繁琐且极少尝试的过程转变成了一个强大的自动化工具,帮助在大数据中发现隐藏的欺诈模式。
Vincent M. Walden, CFE, CPA, 是Kona AI的首席执行官,该公司使命是通过研究驱动的、创新且有效的分析方法,赋予合规、审计和调查专业人士力量,以可衡量的方式减少全球舞弊、腐败和企业风险。他与认证舞弊审查师(CFEs)、内部审计师、合规、审计、法律和财务专业人员密切合作,并欢迎您的反馈和建议。您可以通过 vwalden@konaai.com 联系Walden。
本文由ACFE China校对翻译,如需转载,请提前告知。
原文标题:
Revisiting Benford’s Law with added AI horsepower
By Vincent M. Walden, CFE, CPA
END
关注我们
点击下方 阅读原文 获取ACFE考试评估资格
